Cluster-update recommenders in Monte Carlo simulations

In the previous weeks, we have discussed the classification of phases by supervised and unsupervised learning techniques and the optimization of wavefunction by reinforcement learning. The topic of the current Journal Club is technically rather simple, yet practically very useful: supervised learning for construction of a cluster-updating recommender for Monte Carlo simulations.

Monte Carlo simulation is a numerical method used in a wide array of fields such as natural science, engineering, finance, and statistics. The goal, in general, is to sample data from a given probabilistic model, which is usually the Boltzmann distribution in the context of condensed matter physics and statistical physics.

In systems that are close to critical points, challenges related to the efficiency of the simulation and the independency of the generated data often arise. More concretely, the overcoming the autocorrelation time is a major issue. In some problems the slow-down can be overcome using the so-called cluster-update algorithms. By forming a “cluster” of variables to be flipped, or changed, in a single step, the speed at which the configuration space is explored increases significantly. For 2-body interacting Ising model, for instance, successful examples include the external page Swendsen-Wang (SW) algorithm and external page Wolff algorithm.

What if the system is beyond the applicability of those algorithms (because of complicated interactions, for instance)? Instead of trying to construct a more general and complicated scheme a different route is explored by Junwei Liu et al. [1] and Huang and Wang [2]: to achieve the desired speed-up the configuration proposer, or the recommender, is switched to one based on a simpler and yet ``similar” model so that the cluster-update is valid. This simplified recommender is constructed using ML techniques.

Junwei Liu et al. [1] consider as a test-case the Ising model with additional 4-body interactions on each plaquette, which prohibits the application of the conventional cluster-update methods. In their self-learning Monte Carlo (SLMC) method, one approximates the Hamiltonian by two-body terms including further-neighbors. The coefficients of the new effective Hamiltonian are fixed using simple linear regression. The effective model is used to propose a new spin configuration to the Wolff algorithm, and hence we refer to as “the recommender”.

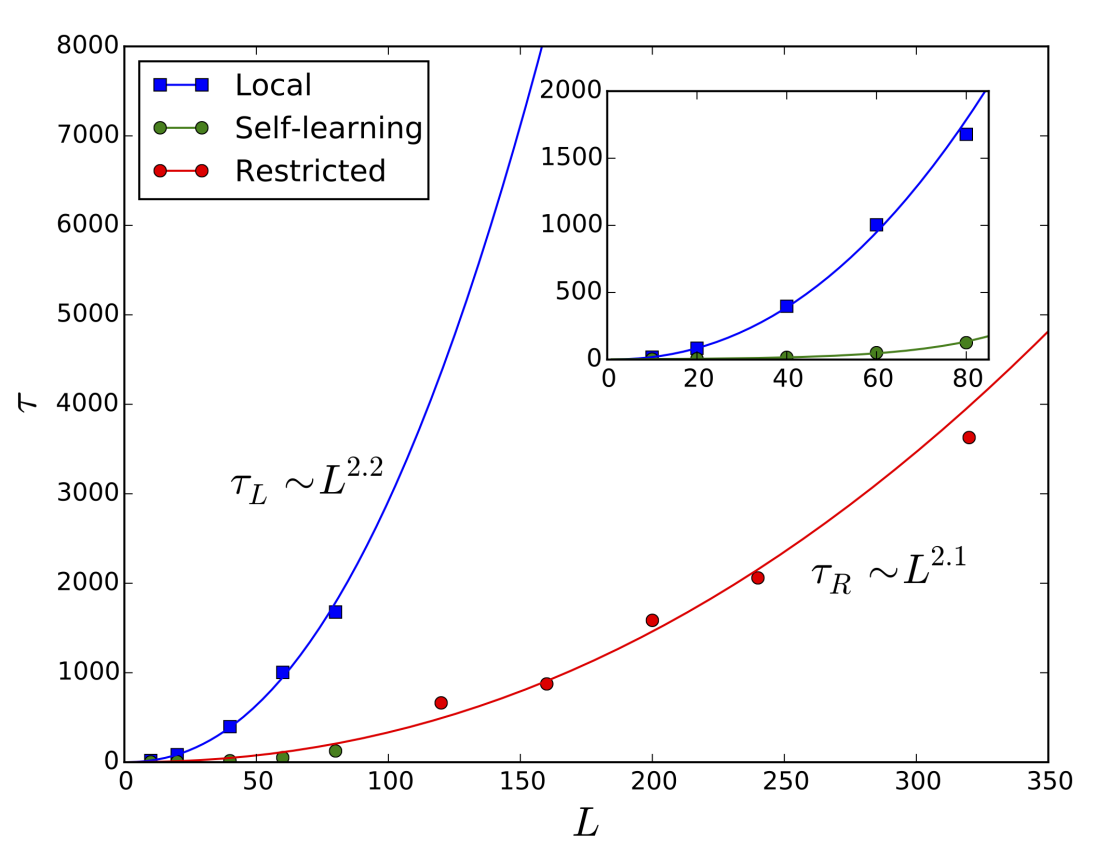
The “accuracy” of the recommender plays a crucial role. Although the Wolff algorithm itself is rejection-free, it is not the case for the original model. Concretely, the difference of Boltzmann factors between the original and effective model must be reflected in the acceptance ratio so that the detailed balance condition holds. For a large cluster, the acceptance ratio decreases exponentially with the length of the cluster boundary (i.e. SLMC also suffers from critical slow-down). The scaling exponent of the autocorrelation time is therefore the same as for local updates. However, by restricting the maximal allowed cluster size the pre-factor can be brought down by an order of magnitude resulting in a promising > 10x speed-up.

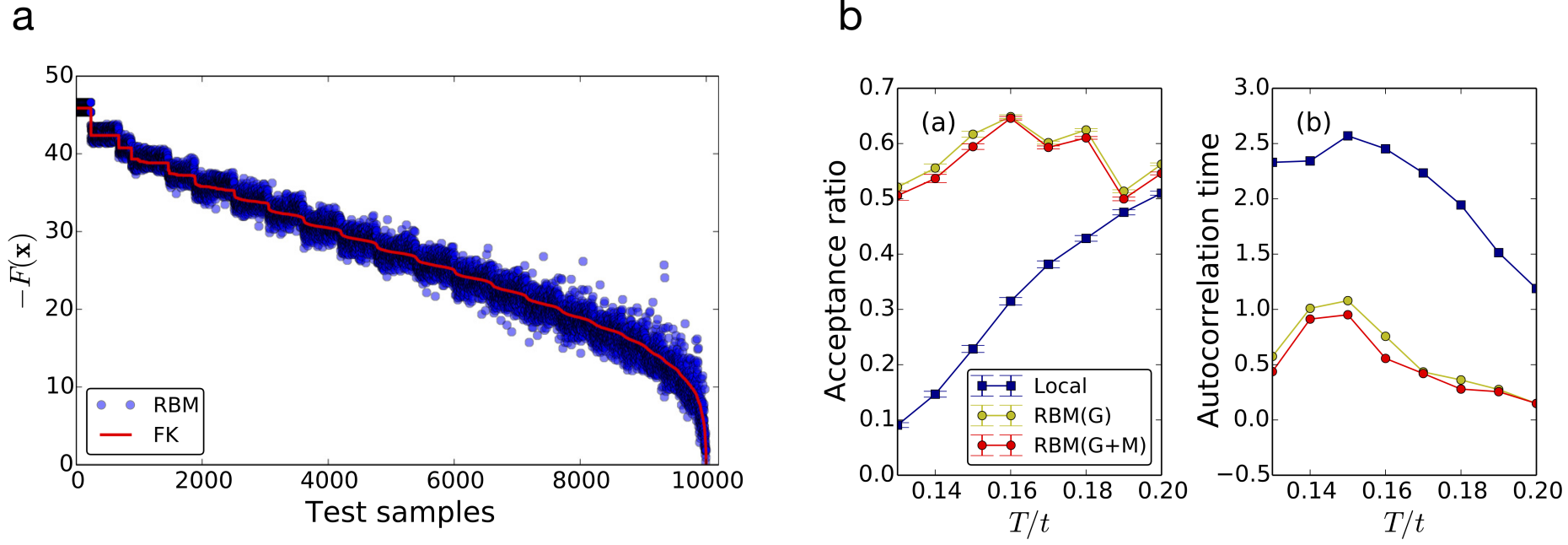
The idea of machine-learning the recommender is more general. Huang and Wang [2] used the Restricted Boltzmann Machines (external page RBM) to propose efficient MC updates. The parameters of the RBM reproducing the free energy of the physical model are learned in a supervised setting, based on data generated with local updates. After training, non-local updates can be suggested by the RBM with high acceptance ratio using the standard Gibbs sampling. The system they considered is the external page Falikov-Kimball model, which describes the mobile and localized fermions interacting on a square lattice. Fig. 2(a) shows the comparison of the Boltzmann factor for configurations of localized fermion, which is obtained by tracing out mobile fermions. The red curve corresponds to the original Hamiltonian and the blue points, which beautifully reproduce the curve, were obtained with the RBM. The autocorrelation time and the acceptance ratio are shown in Fig. 2(b) in comparison with the local-update. Despite the phase transition around T/t=0.15, the acceptance ratio for the RBM recommendation remains higher than the local-update, resulting in less than half autocorrelation time.