Reinforcement learning of the many-body wave function on RBMs
Luca Papariello
In the previous two weeks we saw how neural networks can be used in order to classify different phases of matter of common physical models. Unsupervised learning not only successfully classified the ordered and unordered phases of the Ising model but also gave satisfactory estimates for the critical temperature [1]. Supervised learning and convolutional neural networks managed to investigate more complex systems for which simple networks and PCA were unsuccessful [2]. In their paper, Carleo and Troyer [3] take an orthogonal approach: they introduce a network representation of the many-body wave function and train their network using external page reinforcement learning.
The goal is here -- contrarily to the works discussed previously in this Journal Club -- not the classification of phases, rather the actual solution of quantum many-body problems.
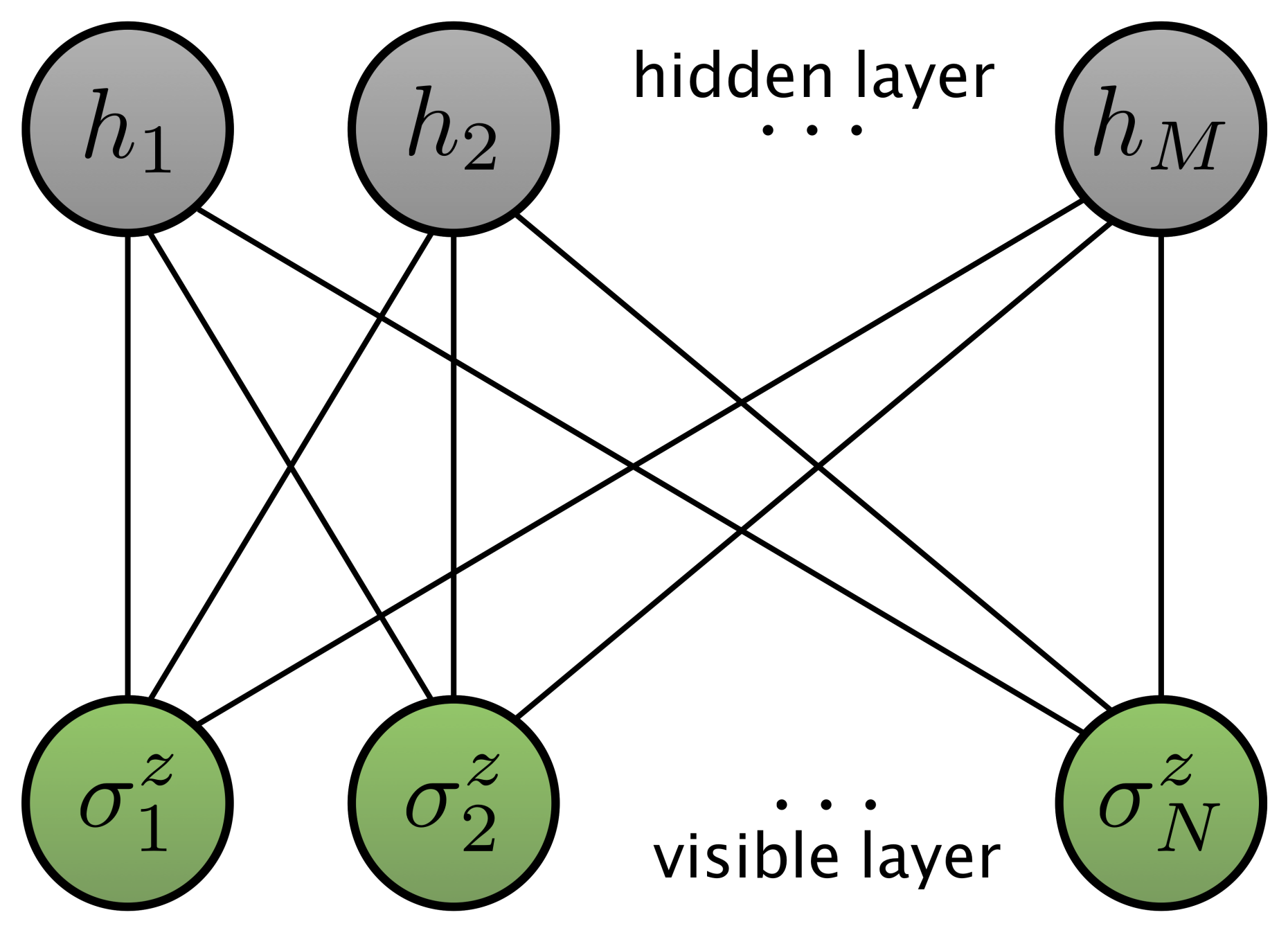
Concretely, they used a specific choice of a machine learning architecture, external page a restricted Boltzmann machine (RBM), as an ansatz for the representation of the wave function (see Fig.1). With this convenient compressed representation of the wave function at hand they were able to find both the ground-state energy as well as the time evolution of two prototypical models: the transverse-field Ising (TFI) model and the anti-ferromagnetic Heisenberg (AFH) model.
Note that it is the specific choice of the network, which only has two layers and does not feature intra-layer connections, that allows for an exact tracing out of the hidden neurons. Note also that here, as opposed to what we have seen so far, the network weights are in general complex-valued.
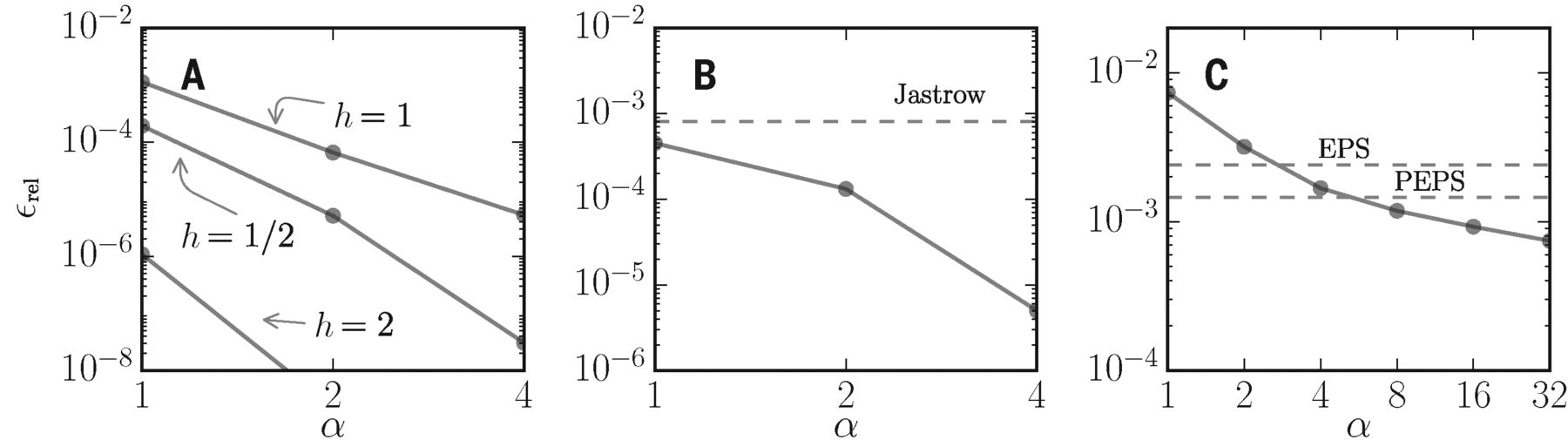
As a first achievement, they show the ground-state energy of the above mentioned models obtained through neural-network quantum states (NQS) as compared to exact results (see Fig.2). Common to all models is the following outcome: a systematic increased accuracy is achievable by increasing the number of hidden neurons M or, equivalently, the hidden variable density (i.e. M/N). Results comparable to state-of-the-art methods can be obtained with relatively small hidden variable density, which provides a more compact representation of the wave function and thus a drastic reduction of the number of variational parameters.
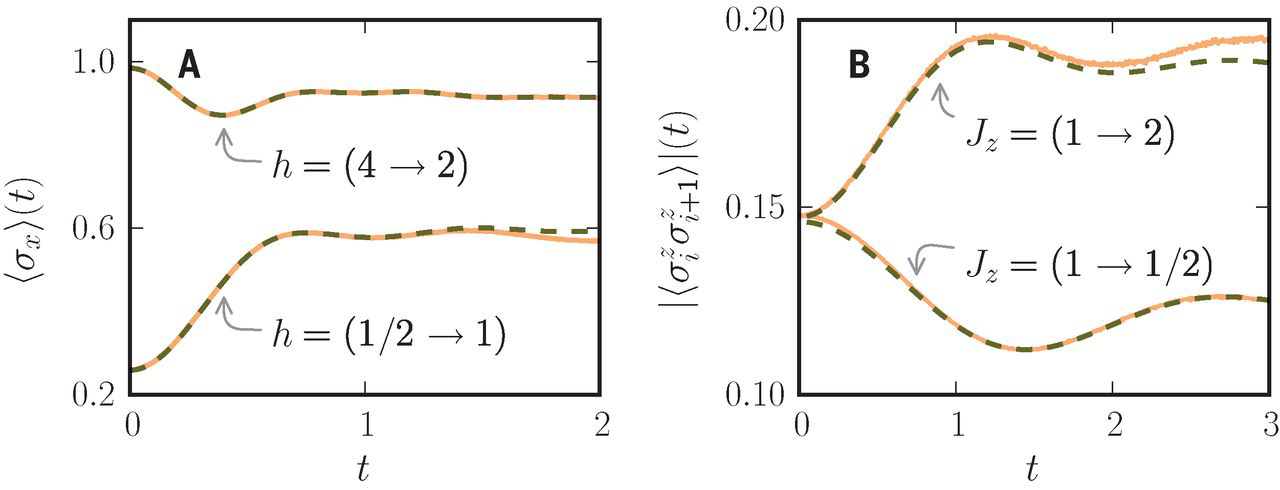
What this RBM can do is not limited to ground-state problems but one can access the unitary time evolution, too (see Fig.3). The figure below shows the unitary time evolution obtained after a quench in the transverse field h and coupling constant J along the z-axis for the TFI and AFH models, respectively. Even though the results are not as accurate as for the ground-state energy, they still get convincing results.
How does the network work? Carleo and Troyer found that the working principle of their NQS is very similar to the one of convolutional neural networks. In their RBM the weight matrix, once trained, take the form of feature filters, in which each filter learns specific features of the data.
So we have seen that a RBM optimized by reinforcement learning provides good results for the presented spin systems. But are there any bounds, or can we get the solution of any many-body Hamiltonian? Yes, there are. Gao and Duan [4] recently proved that there are states, which cannot be efficiently represented by any RBM. The promising extension to deep Boltzmann machines (DBM) overcomes these limitations and seems to be a step in the right direction [5].
- L. Wang, Phys. Rev. B, 94 195105 (2017) external page doi
- J. Carrasquilla and R. Melko, Nature Physics 13, 431 (2017) external page doi
- G. Carleo, M. Troyer, Science 355, 602–606 (2017) external page doi
- X. Gao and L.-M. Duan, Nature Comm. 8, 662 (2017) external page doi
- G. Carleo, Y. Nomura, M. Imada, external page arXiv.