Supervised 'Machine Learning Phases of Matter'
Mark H Fischer
In the previous week, we saw how different phases of matter of simple model systems can be identified using a combination of data analysis and clustering algorithms. In particular, Wei Lang [1] showed how PCA can be used to find the ferromagnetic and paramagnetic phases of the two-dimensional (2D) Ising model. While using more intricate algorithms allowed for the same task to be successfully done for slightly more complicated models, e.g., the previous week's autoencoder on the magnetization-constraint Ising model, many models of interest in condensed matter physics are not accessible within this simple data-analysis / clustering scheme.
It seems a computer cannot map out the phase diagram of a complicated model without further help and, hence, fully replace the condensed matter theorist just yet. This is, however, neither surprising nor should it be the end of the 'classification endeavor': for many model systems, there is ample reason to believe that a significant change of some parameter will result in a change of the system's phase. Most systems undergo a phase transition between a low-temperature phase and a high-temperature phase, to name just the most obvious example.
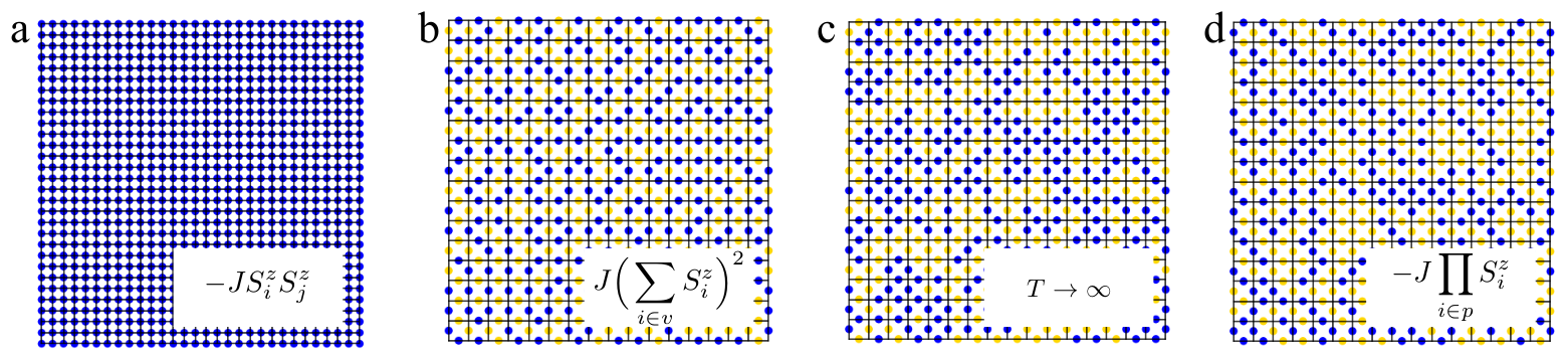
In their paper, Carrasquilla and Melko [2] use artificial neural networks to attack this exact problem: classify low- and high-temperature states and find the 'transition' temperature of three classical spin models of varying complexity, see Fig. 1. Neural Networks are known to be powerful image classifiers, be it for external page hand-written numbers, or simply to external page distinguish cats from dogs. It is thus natural to feed the algorithm pictures, which in the case of (Ising) spin models can be configurations (vectors) of 1's and -1's obtained at different temperatures via Monte Carlo sampling.
But PCA introduced in the previous week not only allows for clustering and identification of phases, it also gives additional information akin to an order parameter. Can a neural network, this infamous black box, also give us any similar insight? In their paper, Carrasquilla and Melko answer this question in the affirmative.
As a first example, they start again with the two-dimensional Ising model as introduced in the previous week (Fig 1a). However, instead of trying to analyze the spin configurations for low- and high-temperature states and use a clustering algorithm, they train a neural network with a single hidden layer to distinguish the two. Using another set of configurations they then find the transition temperature with high accuracy. Interestingly, constructing a toy-model neural network explicitly looking for the total magnetization and comparing it to the trained neural network, they show that the latter indeed learned the Ising model's order parameter.
But can a neural network succeed in a case where there is no order parameter to learn? In order to test the power of neural networks further, Carrasquilla and Melko apply the same scheme to two more models: the Ising square-ice model, and the Ising lattice gauge theory, see Figs. 1b and 1d. These two models do not exhibit a finite temperature phase transition and their ground state, despite being distinct from the high-temperature states, has no order parameter. Moreover, there is a large ground-state degeneracy stemming from the local constraints imposed by the Hamiltonian, see insets of Figs. 1b and 1d, making distinguishing zero- and high-temperature states by eye almost impossible.
Still, the more rigid constraint of the Ising square-ice, namely the two-in / two-out rule, forbids larger clusters of equal spins, in contrast to the lattice-gauge model, where the number of spin ups / downs has to be even, and a random high-temperature state (Fig 1c). Indeed, this difference might be the reason a conventional neural network can be trained to distinguish low- and high-temperature states of the square-ice model. For the lattice-gauge model, however, the conventional neural network fails with a prediction accuracy of 50%, a coin toss.
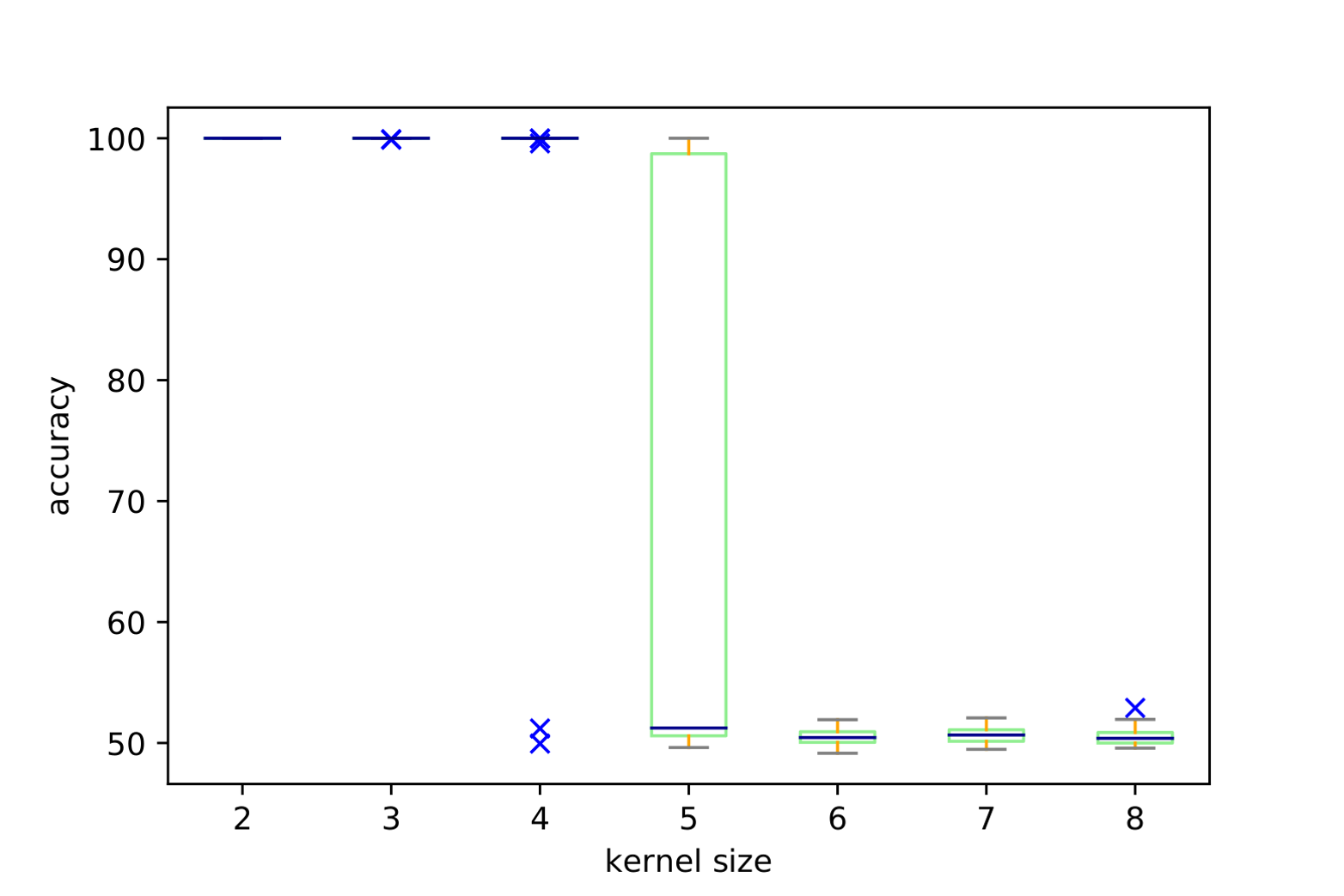
Clearly, discarding all information about the two-dimensional nature of the problem has made it too hard to tackle. Without any geometric information, there is no notion of a local constraint and its translational invariance. For picture classification, retaining information about locality and translational invariance has proven to be a major ingredient, and the external page introduction of convolutional neural networks (CNNs), with filters convoluted with the original picture, has led to a major boost in classification performance. Using 2x2 filters, Carrasquilla and Melko successfully train a CNN to identify low- and high-temperature states of the lattice-gauge model with 100% accuracy (see Fig. 2 to see how the CNN's performance crucially depends on the filter size). Interestingly, the trained CNN predicts a transition temperature corresponding to where thermally-excited defects are of order one. The neural network indeed learns (through its filters) to check for the local constraints. This, again, is nicely illustrated by Carrasquilla and Melko in their work.
So where do we stand now and where do we go from here? Using simple input 'pictures' provided by spin configurations, an artificial neural network can be successfully trained in a supervised fashion to distinguish phases of matter, even in the absence of an order parameter. However, the features learned are 'simple' local features, as exemplified by the lattice gauge model. Further, the authors explicitly refrain from using physical knowledge or intuition for feature engineering. Finally, the input they use, particularly for the last problem they study, localization in the Aubry-Andre model, has significant shortcomings. A natural extension is thus to use different input data, e.g., Green's functions [3], or entanglement spectra [4]. Still, the paper by Carrasquilla and Melko provides a very nice proof of concept and their collection of problems a wonderful sandbox to try out the various networks yourself (see for example external page my git if you would like to get started).
- L. Wang, Phys. Rev. B, 94 195105 (2017) external page doi
- J. Carrasquilla and R. Melko, Nature Physics 13, 431 (2017) external page doi
- P. Broecker et al., Scientific Reports 7, 8823 (2017) external page doi
- E. van Nieuwenburg et al., Nature Physics 13, 43 (2017) external page doi