From PCA to Variational Autoencoders
Sebastian Huber
Classifying thermodynamic phases and transitions between them is one of the main tasks of a condensed matter researcher. Given a set of measurements, we try to identify special temperatures or values of other tuning parameters at which the behavior of a physical system undergoes a qualitative change. In his paper, Lei Wang explores how this task of identifying phases can be delegated to an autonomous, or unsupervised algorithm.
Arguably the simplest technique to analyze large data sets is the external page principle component anlysis (PCA). Given a set of n samples of d measurements, PCA finds the linear transformation in the d-dimensional measurement-space such that the samples differ the most along the first, second, etc. direction in the new coordinate system. Imagine that the n samples correspond to sets of d physical measurements obtained on different sides of a phase transitions.
Lei Wang's key idea is that PCA applied to all these measurements should single out the linear combination of measurements which differs the most in the two phases. One could call this strategy successul if a simple clustering method like external page K-means produces well-defined clusters in the reduced space of the first few principle components. If successful, this approach offers a neat insight: the linear map to the first principle component indicates a physical order parameter.
Lei Wang applies his idea to one of the drosophilas of statistical mechanics: the two-dimensional Ising model where neighboring spins (si=±1) on a square lattice gain an energy J if they take the same value and pay -J if they differ. Below a critical temperature of T ≈ 2.27 J/kB, a net magnetizatio m=∑i si is buidling up. And indeed, if many Monte Carlo samples of different temperatures are fed to PCA, it identifies the magnetization as the first component and K-means forms clusters as shown below.
The performance of PCA on the Ising model is impressive. But it is intereting to test where PCA fails. Lei Wang considers again the Ising model, but this time at fixed magnetization m=0. Clearly the magnetization cannot serve as an order-parameter. However, the system still undergoes a phase transition where horizontally or vertically magnetized stripes appear. The order parameter for this phase is the Fourier-component of the spin-spin correlation function with a wavelength equal to the system size. In his paper Lei Wang discusses how this order-parameter is not linearly related to the bare Monte-Carlo data and hence linear PCA cannot detect it.
In the machine learning community, PCA is often mentioned in conjunction with external page autoencoders. In particular, variational autoencoders learn a latent variable model. In essence, the algorithm is trying to learn a probability distribution, conditioned on a few latent variables (See external page arXiv:1606.05908 for a nice introduction to the idea). These latent variables can be seen as a generalization of the first few principle components of PCA. The strength of this approach is two-fold: First, it can leverage the non-linear power of a feed-forward neural network. Second, having learnt a probabilistic model, one can generate new samples using the variational autoencoder. In condensed matter physics, Sebastian Wetzel pioneered the use of variational autoencoders in his recent publication in Physical Review E.
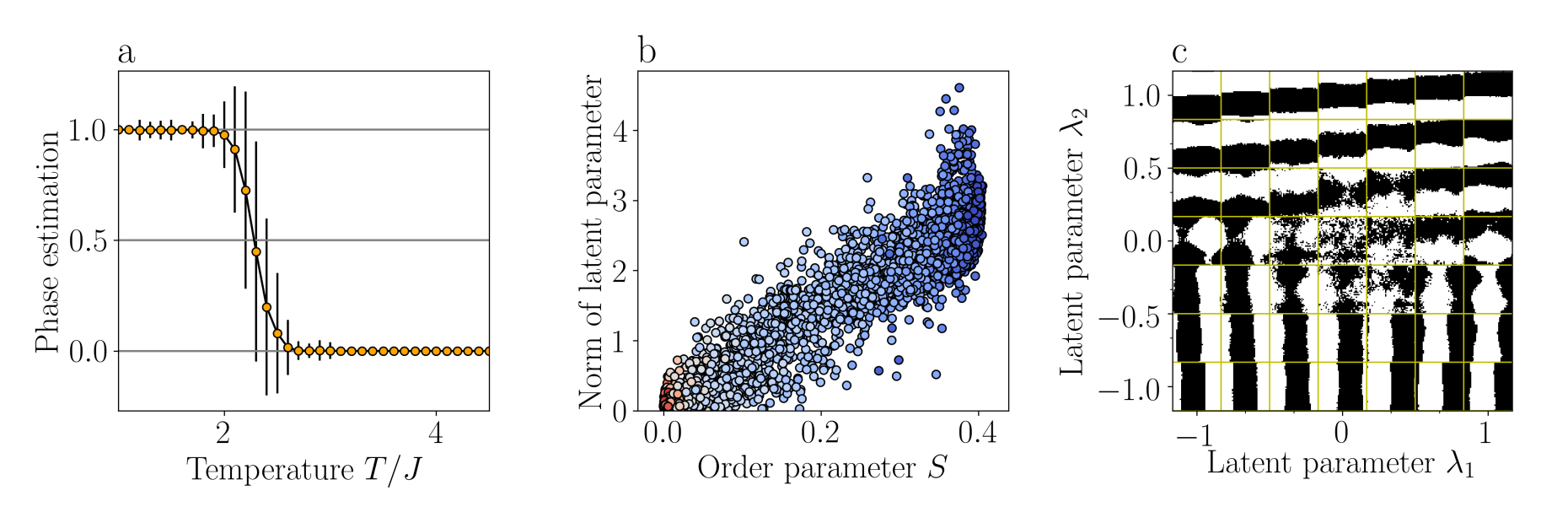
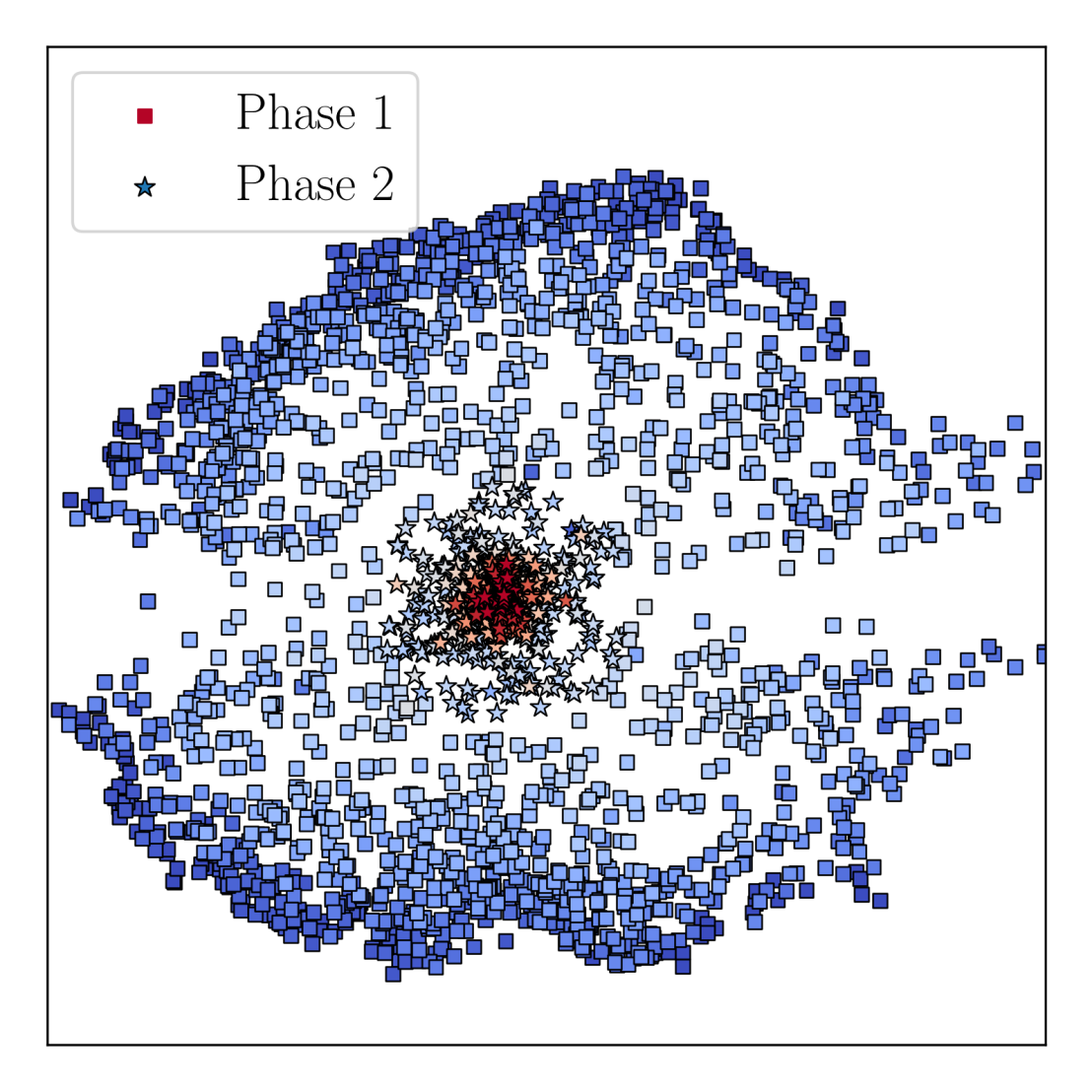
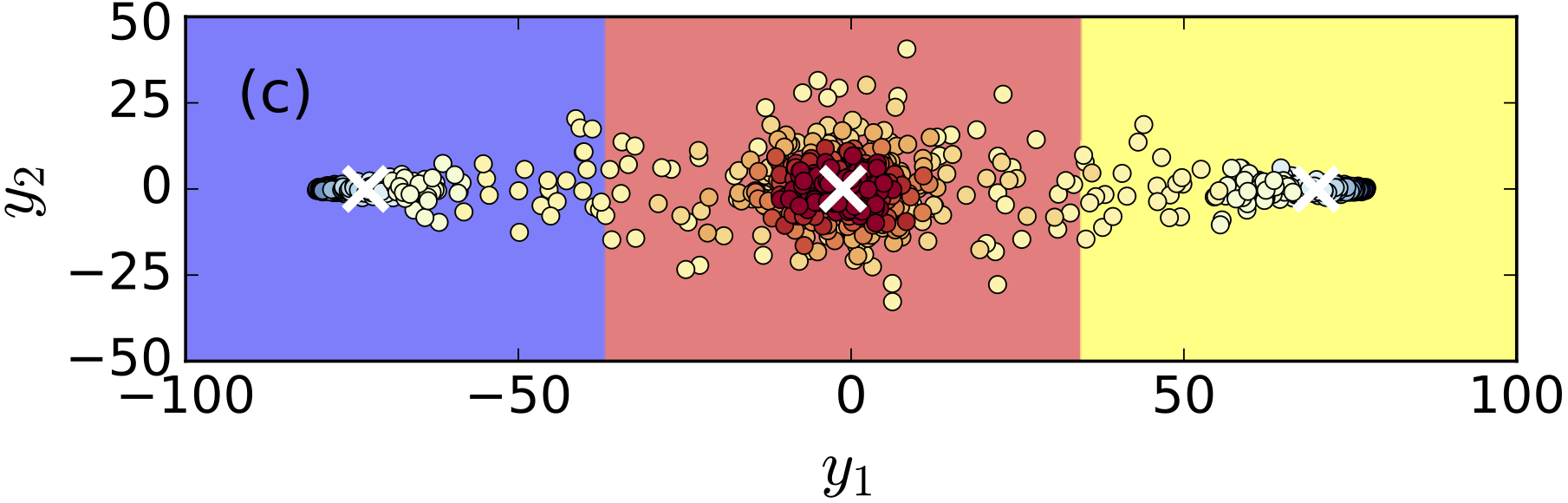
Here we want to explore if variational autoencoders can detect the phase transition in the fixed mangetization Ising model where linear PCA failed. The short answer is: yes, it can! Fig. 1 above shows how k-means clusters samples in the two-dimensional latent space of a variational autoencoder. We generate many such images and calculate the probability to which phase the algorithm assignes a sample from a given temperature. The results is shown in Fig 3a. The reason for the success can be assigned to the fact that the absolute value of the latent variable seems to be well correlated with the order parameter, cf. Fig 3b. Finally, samples generated from the latent variable model are shown in Fig 3c. Clearly, the autoencoder latches on the right physics.
The variational autoencoder used here is an adaptation from the external page Keras blog. We classify Monte-Carlo samples of a lattice of size 40x40 sites, which we obtain from a simple pair-flipping Metropolis algorithm. Both the encoder and the decoder are built with a dense layer of 256 neurons and we employ a latent variable model with two latent variables. We train the network with 105 samples and use another 105 for the clustering with K-means from external page scikit-learn. All codes needed to reproduce Figs. 1&3 are available on external page github.
What did we learn from the two papers by Lei Wang and Sebastian Wetzel? Certainly the reduction of complexity PCA can offer can guide us in finding phase transitions. However, linear PCA already fails on a fairly simple model, the conserved order parameter Ising model. Variational autoencoders can perform where PCA doesn't. While this is promising, the road to a fully autonomous unsupervised detection of a phase transition that we did not know before seems still to be a long one. Moreover, on the external page Ising gauge theory also the variational autoencoder seems to fail. At least we didn't manage to get it going, neither with multi-layer feed-forward architectures nor with deep convolutional networks.
- L. Wang, Phys. Rev. B, 94 195105 (2017) external page doi
- S.J. Wetzel, Phys. Rev. E, 96 022140 (2017) external page doi