Machine learning topological phases

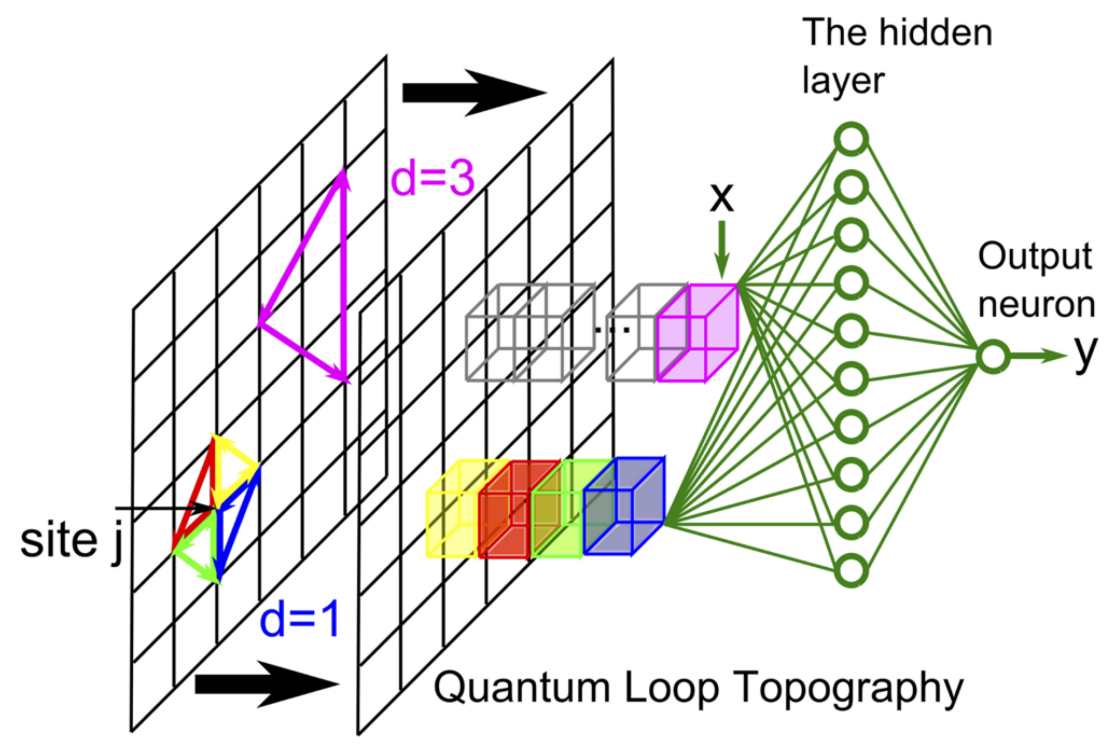
A useful hint comes from a different formulation by Kitaev [5] of the Hall conductivity, that we know characterizes the Chern insulator.
This response function can be written as the sum over products of two points correlation functions that form a triangular loop. Therefore, one could provide as an input to the neural network a vector for each lattice site containing all the possible triangular loops of non averaged two-points correlation functions that have a vertex on that lattice site. This is the procedure that the authors call "quantum loop topography" (QLT), schematically presented in Fig. 1 . In principle, the sum in Kitaev's formula extends over all the possible triangles. However, in presence of gapped systems away from the phase transition, the correlation lengths decay exponentially  and one can set a cutoff on the maximum triangle size. The results presented in Fig. 2a show how a fully connected neural network successfully learns the phases of the model already with 10 hidden neurons and a maximum triangles size of 2.

How should we judge the performance of this approach? One could argue that the strucutre of the provided data was strongly based on the quantity that is known to characterize the phase under study, Kitaev's formula for the Chern number. Its power lies in the abilitity to generalize! The authors apply QLT to a fractional Chern insulator. They sample from the same variational wavefunction of the Chern insulator but elevated to the cubic power. In this case, the formula for the Hall conductivity provided by Kitaev does not hold. However, they are successful in classifying the two phases of the model, Fig. 2b. As expected, the neural network also captures the ground state degeneracy even when trained on a single ground state configuration.  

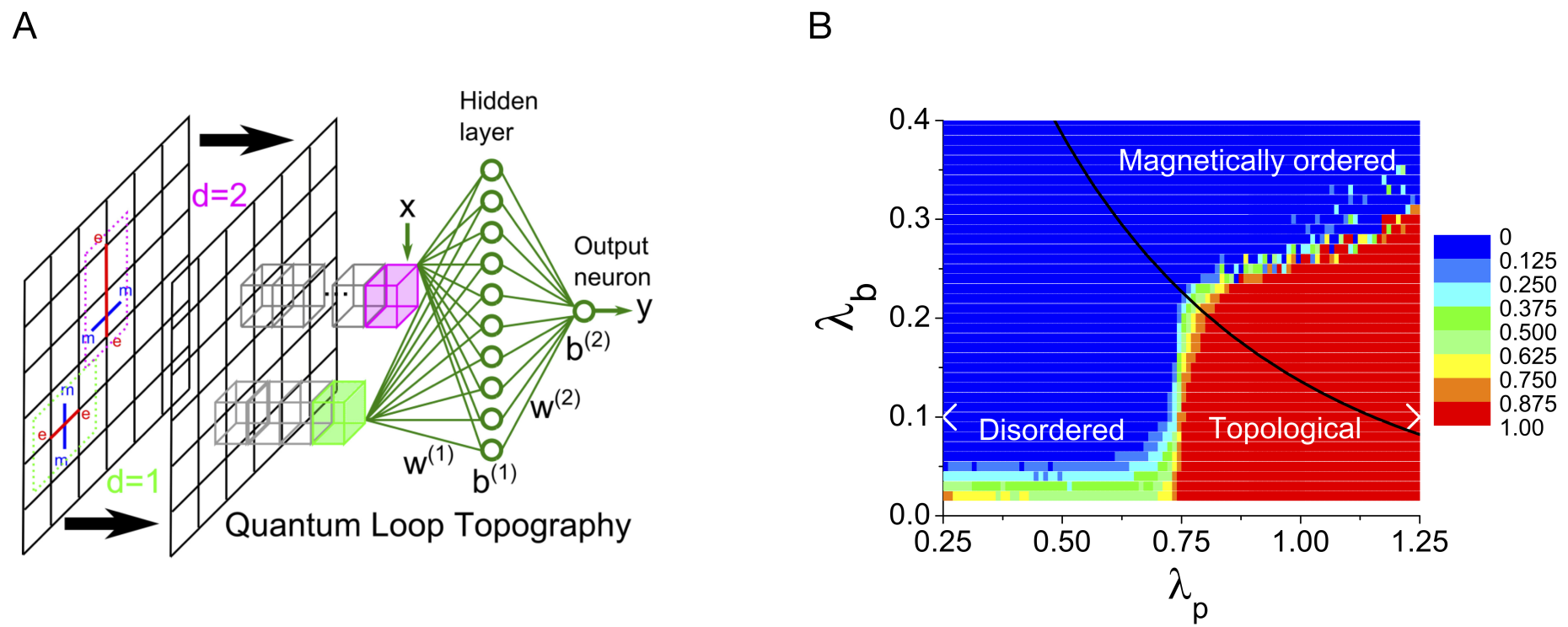
In a follow up paper [6], the authors further extend QLT to a non-chiral phase: the toric code in an external field [6]. Here they consider as input data loops of quasiparticles excitation as schematically shown in Fig. 3a. Again, by feeding the neural network with minimally non-local information that characterize the phase, the authors succeed in learning the phase diagram of the model under consideration, as shown in Fig. 3b.

We have seen how a simple fully-connected neural network can be trained to learn topological phases of matter with a little help from the human side. QLT provides a useful tool to interface response functions theory and machine learning for phase classification. Moreover, it is a fully real space technique that could be suitable to tackle disordered systems. However, there are few question that have not yet been addressed. It would be interesting to look at the weights of the neural network to see what it actually learns in the different cases. It would also be interesting to quantify how much knowledge of the phase under study is needed. How would the neural network perform if we feed it with just two point correlation functions instead of triangular loops? Answering these questions could provide a further advancement in the use of machine learning to tackle topological phases of matter.