Topological sound without symmetries

Topological insulators, initially studied in the materials community, are attracting growing interest in other fields like optics and acoustics. There, rather than electrons, electromagnetic and acoustic waves propagate in a periodic array of scatterers. The beauty of universality make sure that also in these platforms robust, scatter-free waveguides confined at the sample's edges appear.

One way to obtain topological edge modes is to break time reversal symmetry and realize a Chern insulator. Nonetheless, this is unfeasible in passive classical metamaterials. Alternatively, one could try to mimic the physics of a spin Hall insulator. This is also unnatural for low-energy bosonic excitations as a fermionic time reversal symmetry is required.

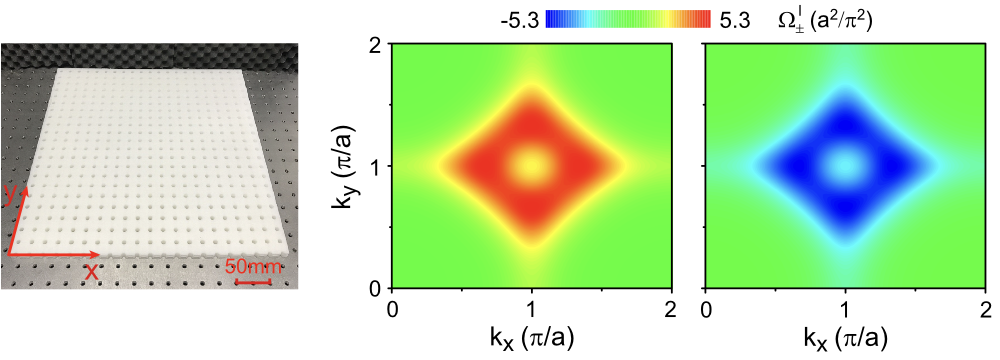
In this work, we realize and experimentally characterize an acoustic metamaterial whose non-trivial topology and edge states can be captured in the absence of any symmetry via a "spin"-Chern number. Thereby, we validate the spin Chern number as a useful topological invariant for classical metamaterials. Moreover, in a H shaped device, we demonstrate how the edge modes path can be tuned by geometry, enabling the construction of robust and complex networks.