Machine Learning with Tensor Networks
Eliska Greplova
Until now, this blog has been discussing machine learning based on artificial neural networks (ANNs). This means that we implement a map composed by a network of neurons, which is the trained by means of the back-propagation algorithm. The paper [1], which is the main topic of this blog post, offers a new alternative for training which is intimately related to standard tools used in the field of many-body physics. In [1], the authors show that a tensor network can be trained by sweeps similar to external page DMRG (density-matrix renormalisation group) and the method performs well on the set of standard machine learning tasks.
More specifically, the algorithm proposed in the paper finds a matrix product state (external page MPS) representation that minimises a generic loss function. MPS is a tool that has been widely and successfully applied in many-body physics [2] and is based on the assumption that physically relevant many-body states do not require a description that scales exponentially with the system size, but cleverly chosen one with polynomial number of coefficients suffices. This method has been successfully used to tackle number of many-body problems in 1D.
The authors of the present paper argue that MPS is a natural platform to encode physical systems and machine learning can be performed directly within the realm of the tensor network. In addition to that, the authors make a claim that “training the model scales linearly in the training set size and the cost of evaluation an input is independent of training set size”.
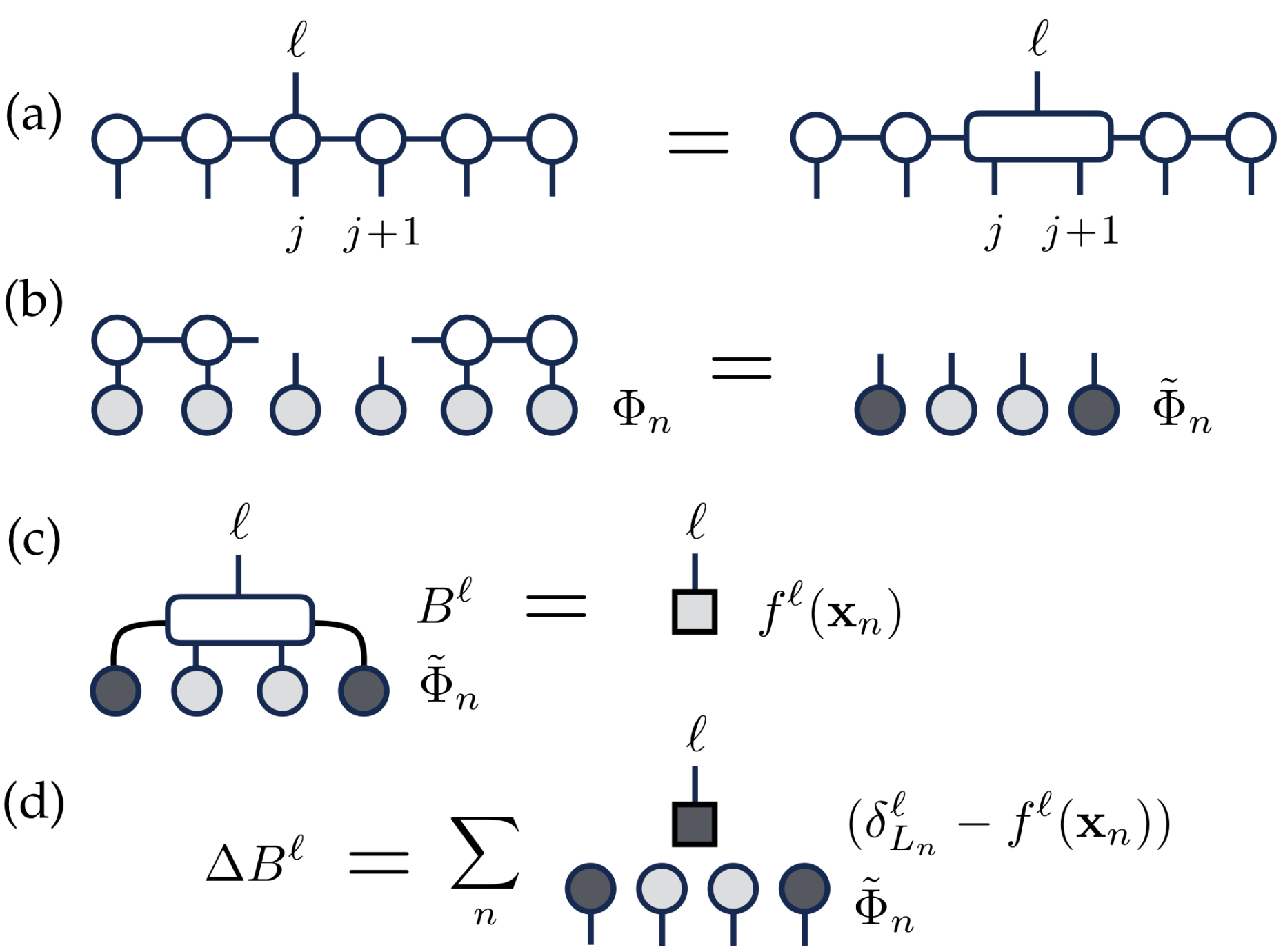
The goal in machine learning is in general to minimise a loss function, which can be done using a gradient descent algorithm. By contracting the tensor-network, the gradient of the loss can be found. The DMRG-like sweep proposed in this work works as follows: In each step of the sweep, the tensors are changed to reduce the loss function and the extra bond is moved from site j to site j+1. In particular, the sweeps are realised in 4 steps as shown in Fig. 1. Firstly, a bond tensor of two neighbouring sites, j and j+1, is made (a). Then the projection on the local basis is calculated (b) which is needed to calculate the loss function (c) and gradient of the bond tensor (d). The correction to the bond tensor based on gradient criterion is added and then the bond is decomposed into the MPS form using a singular-value decomposition. This procedure is then repeated for the next site and the whole MPS is swept backward and forward until the cost function is minimised.
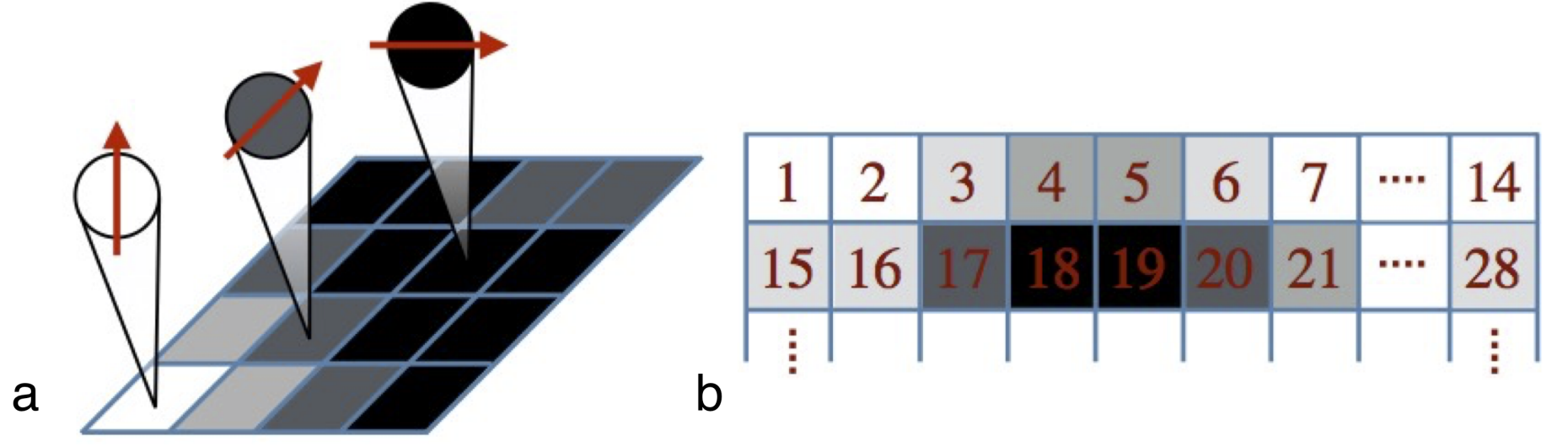
The tensor network machine learning is illustrated on two example problems: external page MNIST and boundary decision. In the MNIST case, the first thing we immediately realise is that the input data are not in the MPS form, so the encoding mapping has to be constructed at first. The example of this mapping is illustrated in Fig. 2 (a), where the greyscale value of each pixel is encoded into “spin” direction via trigonometric map. This array is then reshaped into 1D spin chain that can be efficiently described in MPS terms (see Fig. 2 (b)).
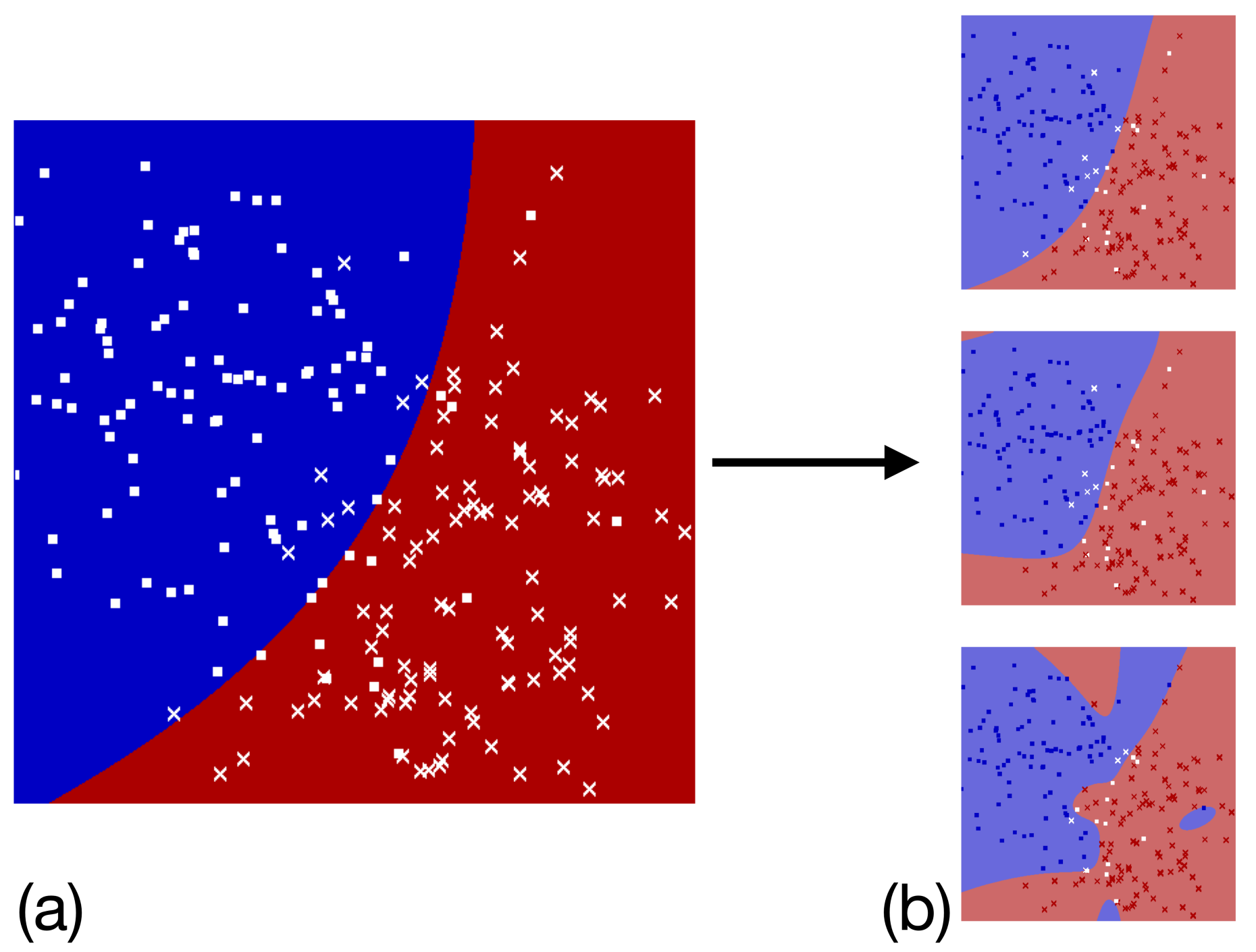
Another simple illustration of this method is a boundary decision problem. Consider multivariate Gaussian distributions as illustrated in Fig. 3 (a), where we can see training points that were sampled from two multivariate Gaussian distributions and the optimal theoretically calculated decision boundary. The results learned by the network for different choices of bond dimension are shown in Fig. 3 (b).
This work definitely brings new figure of merit to machine learning: that the training can be done directly within the tensor networks that are used to efficiently describe many-body states. The construction and training of the neural network in the present work was done using the external page iTensor library. We are looking forward to see how this method performs in more complex context and whether it can be benchmarked against commonly used neural network methods. Our attempt to reproduce the algorithm of the paper using standard machine learning library, external page Tensorflow, was successful without preserving the linear scaling of the approach described in the present work. It would be very interesting to see if there is some general advantage in tensor network encoding that can be use with advantage in the many-body context.
- E. M. Stoudenmire, D. J. Schwab, external page arXiv:1605.05775 (2017)
- U. Schollwoeck, Annals of Physics, 326, 96 (2011) external page doi