Machine learning in condensed matter physics
Maciej Koch-Janusz
Welcome to Machine Learning in Condensed Matter Journal Club at the Institute for Theoretical Physics of the ETH Zurich. This blog is a companion to, and summary of, the talks given weekly for the JC organized by Sebastian Huber, Mark Fischer and myself. The idea of this JC is to allow the participants the familiarize themselves with, and to acquire a topical overview of, the important contributions to this fast growing but extremely young field (the bulk of works are less than 2 years old at this point).
Let us begin by addressing the elephant in the room and posing the obvious question — why machine learning? Is this all just a rather tasteless fad? The answer is no, or, more precisely, that among all the trivialities and hype there are gems to be found. Through a combination of theoretical developments and practical progress of computing architectures, machine learning had in the last decade crossed a threshold which allowed it to deliver a number of impressive results in various fields such as automated translation, image and voice recognition, or game-playing. It is only natural to ask whether some of the techniques employed can lend themselves to fundamental research, in particular to condensed matter/statistical physics.
We believe the results already obtained and the future outlook justify a serious interest in this field. At the same time it is important to realize that ML is largely a result-driven field dominated by engineering approaches, and, ultimately, the goals of an engineer and a scientist are different. As theoretical physicists, we find the increase in, say, correct classification from 93% to 94% achieved by hugely more complicated architectures marginally relevant, important for applications (and business) though it may be. On the other hand we are in the business of understanding, and therefore results explaining the relations between features extracted by ML algorithms and correlations functions, order parameters etc. or principled estimates and bounds on performance are much more interesting (though, to be fair, the recently fashionable idea of “explainable AI” seems like a step in the right direction).
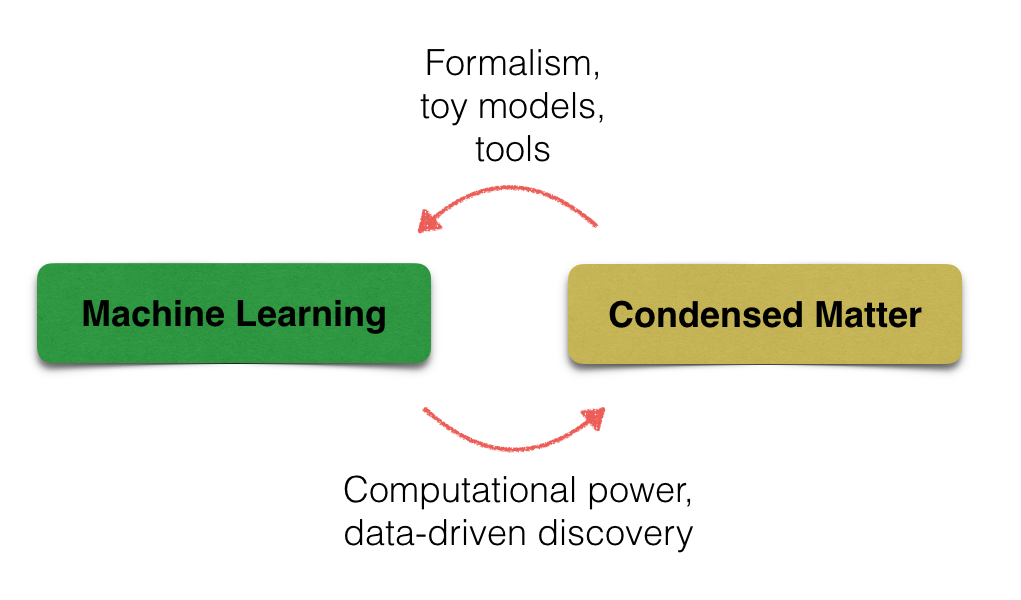
It is thus fair to conclude that there could be (and, to an extent, there has been, for decades already) a mutually beneficial relation between condensed matter and statistical physics, and machine learning. This relation is schematically shown in Fig.1. Physics, one hopes, stands to gain from application of new computational/data analysis methods (more on that below). Conversely, the field of machine learning and AI could benefit from application of powerful techniques of statistical physics (see Ref.[1] for instance) and also from a physicists’ approach to problem solving - constructing toy models, analyzing essential features of the phenomena qualitatively on well-understood examples, without diving head-first into massive and poorly characterized data sets. This is not entirely an altruistic point of view — a deep understanding of performance and behavior of machine learning algorithms is essential for recognition and serious adoption in theoretical physics community, currently rather skeptical partly due to the “black box” stigma ML carries. Let’s get on with it!
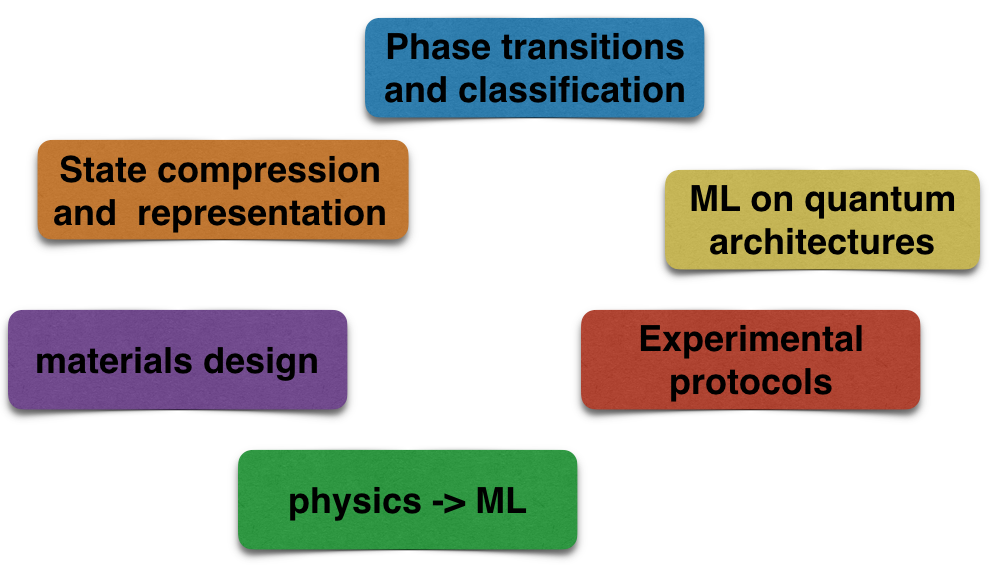
In Fig. 2 we put up a tentative (and admittedly arbitrary) classification of the majority of papers published in the last two years on ML in condensed matter. We have identified, based on the subject matter, or techniques employed five to six main groups, ranging from fully experimental data-mining approaches to theoretical and numerical advances. We will try to explore them in the Journal Club in the coming weeks.
Perhaps the best represented among recent works are those pertaining to the problem of phase and phase transitiond iscrimination/classification (see eg. Refs. [2-5]). The approaches vary both in the scope of methods (everything from PCA and Boltzmann machines to Conv-Nets and LSTMs), and the data sets employed, which can be raw Monte Carlo samples, entanglement spectra, magnetization snapshots etc. Another interesting direction is providing compressed representations of quantum wave-functions, from which ground-state or dynamical properties can be extracted (see Ref. [6]).
ML is used to optimize experimental measurements protocols [7] and to speed-up more traditional numerical techniques, eg. Monte Carlo simulations [8,9]. It also features prominently in new material design strategies [10].
A somewhat orthogonal direction is the application of the theoretical and numerical techniques developed for the study of quantum systems (tensor networks, for instance) to more traditional machine learning problems, such as image classification [11]. Finally, performing ML on quantum architectures has also been explored (see the review [12]).
With this — necessarily brief — summary let us conclude. A fuller picture will emerge as we progress, which hopefully would find its way to this blog in due time. Looking forward!
- H. S. Seung, H. Sompolinsky, and N. Tishby, Phys. Rev. A 45, 6056 (1992) external page doi
- Lei Wang, Phys. Rev. B 94, 195105 (2016) external page doi
- J. Carrasquilla and R. Melko, Nature Physics 13, 431–434 (2017) external page doi
- E.P. van Nieuwenburg, Y. Liu, S. Huber, Nature Physics 13, 435–439 (2017) external page doi
- Schoenholz et al., Nature 12, 469–471 (2016) external page doi
- G. Carleo, M. Troyer, Science 355, 602–606 (2017) external page doi
- A. Hentschel, B.Sanders, Phys. Rev. Lett. 104, 063603 (2010) external page doi
- Li Huang and Lei Wang, Phys. Rev. B 95, 035105 (2017) external page doi
- Junwei Liu, Yang Qi, Zi Yang Meng, and Liang Fu, Phys. Rev. B 95, 041101(R) (2017) external page doi
- Raccuglia et al. Nature 533, 73–76 (2016) external page doi
- M. Stoudenmire, D. Schwab, external page Advances in Neural Information Processing Systems 29, 4799 (2016)
- Biamonte, Wittek, Pancotti, Rebentrost, Wiebe, Lloyd, Nature 549, 195–202 (2017) external page doi